Analýza výsledků modelu
Interpretace spočtených standardů
Na výstupní informace výpočtu je zapotřebí pohlížet
v absolutním měřítku jako na trendy vývoje součástí modelu v čase. Je
tedy zřejmé, které prvky se rozvíjejí pozitivně, které negativně, které
přispívají k celkovému pozitivnímu rozvoji modelu a udržují jeho
standard na uspokojivé úrovni a které naopak modelu škodí a strhávají s
sebou následně i ostatní části modelu.
Grafická forma výstupů je podložená číselným základem,
který poslouží zejména v případech, kdy jsou průběhy výsledných
hodnot do značné míry podobné nebo se v některých intervalech v grafickém
výstupu na první pohled překrývají.
Druhy analýzy
Vypočtené výsledky jsou zpracovávány vzhledem k dalším
zásahům dvěma základními způsoby:
a) manuální postup analýzy
b) automatická analýza výsledků.
Obě varianty se používají odděleně v jiných situacích.
První z nich je prováděna samotným řešitelem úlohy, který se v daném
okamžiku stává expertem analyzujícím samostatně výsledky Xi(t).
Případně může být zprostředkovatelem výsledků analýzy, kterou
zpracoval skutečný odborník na vybranou oblast. Druhý postup je prováděn
automaticky na základě definovaných procedur.
Je nutné si uvědomit k čemu má být analýza výsledků
Xi(t) určena. Jednotlivé cíle pak ovlivňují její strukturu a
podrobnost. Při sledování rámcových (globálních) cílů není nutné
zkoumat hodnoty do nejmenších detailů. Naopak při podrobném ladění a
zjišťování limitního chování modelu musí být podrobnost analýzy
dostatečně vysoká. V opačném případě její závěry nepovedou efektivně
správným směrem nebo správné řešení zůstane mimo směr opatření,
která vycházela z těchto závěrů.
Manuální postup analýzy bude postačující použít v
případě, kdy budeme sledovat globální vývoj modelu. Je tedy vhodné
rozhodnout zda analyzovat chování modelu jako celku nebo konkrétně
zvolenou část. V prvém případě mohou být požadavky na vývoj například
následující:
-
udržení pozitivního vývoje celého modelu
-
udržení negativního vývoje celého modelu
-
udržení vývoje modelu nad zvolenou minimální
hladinou
-
udržení vývoje modelu pod zvolenou minimální
hladinou.
Popsané cíle neobsahují jistě konečnou množinu požadavků
kladených na výsledné chování. V každém řešeném případě budou jiné
a budou mít i jiné preference. je možné je aplikovat na všechny prvky současně
nebo z nich sestavit příbuzné ucelené části a na ně uplatňovat opatření
vzešlé ze závěrů analýzy. Taková agregace může přispět k průhlednějšímu
řešení a lépe prokázat účinnost zvolených zásahů.
Při manuálním způsobu analýzy vzhledem k požadavků
na celkový vývoj ji není možné provádět průběžně. Řešitel by
musel vždy po vypočtení aktuálně zpracovávaného okamžiku výpočet přerušit
a provést analýzu. Podle jejích závěrů pak rozhodnout zda pokračovat dále
nebo výpočet naprosto zastavit a po zavedení zásahů začít opět od začátku.
Je vidět, že tyto okolnosti mohou značně prodloužit dobu zpracování a
proto byly řešeny a odstraněny v automatické analýze popsané dále.
Analýza celkového vývoje se skládá z analýz dílčích
částí modelu . Při provádění rozboru konkrétního prvku Xi
se situace zjednodušuje. Požadavky na chování dílčí části modelu,
kterou má analýza sledovat mohou být obdobné jako požadavky na celkový vývoj:
-
udržení pozitivního vývoje dílčí části modelu
-
udržení negativního vývoje dílčí části modelu
-
udržení vývoje vybraného prvku modelu nad zvolenou
minimální hladinou
-
udržení vývoje vybraného prvku pod zvolenou minimální
hladinou
-
dosažení požadovaného průběhu vývoje chování.
Při manuální analýze dílčího prvku Xi se
sleduje tedy již konkrétní část modelu vzhledem ke zvoleným požadavkům.
Opět je zde problém s prováděním průběžného rozboru stavu jako při
variantě globální analýzy všech prvků.
Novou možností je dosažení požadovaného průběhu vývoje.
Za pomoci externích vlivů je možné dosáhnout posunu vývoje do předem
vytyčeného prostoru - feasibilní plochy. Okamžik pro zavedení zásahu musí
řešitel vystihnout samostatně stejně jako jeho intenzitu. Po novém propočtu
ověří účinnost navržených opatření na základě analýzy vývoje.
Automatická analýza provádí obdobné procedury jako
manuální varianta. Zásadní rozdíl je v tom, že veškerá vyhodnocení řeší
výpočetní aparát samostatně na základě předem nadefinovaných kritérií.
Tyto informace upřesňují jaké prvky Xi a jakým způsobem má
analýza sledovat a vyhodnocovat. Opět je možné provést globální rozbor
celého modelu nebo jeho konkrétní části. Druhy automatické analýzy jsou
zpracovány následující:
-
analýza vývoje při zadané minimální hladině
-
analýza vývoje při zadané maximální hladině
-
analýza vývoje při zadané feasibilní ploše
(prostoru) vývoje
-
analýza dosažení požadované hodnoty.
Stejně jako manuální provádění analýzy i automatická
analýza celého modelu se skládá z analýz jednotlivých jeho částí.
Analýza při zadané minimální hladině MIN se užívá
při řízení modelu takovým způsobem, aby všechny části (případně
konkrétně vybraný prvek) neklesly při svém vývoji pod tuto hranici. Na
rozdíl od manuální varianty je systém schopen sledovat vývoj průběžně
a tvořit závěry na jejichž základě se budou stavět následná opatření.
Nutné informace pro analýzu minimální hranice jsou následující:
- vybraný prvek Xi - hodnota minimální hranice MIN.
Princip analýzy spočívá v průběžném sledování číselných
hodnot vývoje Xi(t) v reálném čase a poskytování odpovědí
na analyzovanou otázku. V tomto případě na otázku, zda již byl dosažen
pokles pod minimální zadanou hladinu (Xi(t)<MIN). Aparát,
který navazuje na závěry analýzy, pak musí reagovat na získané
informace správným způsobem. Pro udržení minimálního vývoje bude zapotřebí
posílit nejvíce negativní části modelu, případně zavést nové externí
vlivy. Vyhodnocení poklesu pod MIN uvádí obr. 1.

Obr. 1 Vyhodnocení poklesu pod zadanou minimální hladinu
MIN. Ve vyznačeném okamžiku analýza vývoje podává informace o poklesu
pod zadané minimum (Xi(t)<MIN). Další zásahy musí reagovat
pozitivním způsobem na odstranění tohoto jevu
Tendence ve vývoji modelu mohou ale být naprosto opačné.
Analogií analýzy minimální hranice je sledování a vyhodnocování maximálního
standardu prvku Xi. Cílem je tedy udržení vývoje celého modelu
nebo jeho konkrétní části pod zadanou maximální hladinou MAX. Nutné
informace pro sledování maximální zadané hranice jsou následující:
-
vybraný prvek Xi
-
hodnota maximální hranice MAX.
Princip analýzy spočívá ve sledování a testování
vypočtených hodnot standardů prvků v reálném čase se zadaným maximem.
Výsledky testů jsou poskytovány následnému výpočetnímu aparátu, který
na ně musí zareagovat.Pro potlačení pozitivního vývoje prvků bude zapotřebí
redukovat kladné vlivy přicházející od ostatních prvků. Další zpracování
je otázkou řízení modelu. Schematicky je vyhodnocování uvedeno na obr.
2.
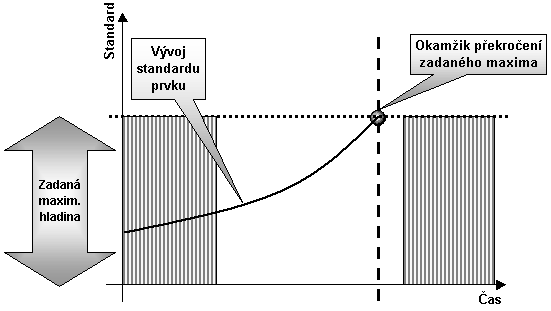
Obr.
2 Vyhodnocení překročení zadané maximální hladiny MAX. V okamžiku překročení
maximální zadané hranice analýza informuje o této situaci (Xi(t)>MAX)
a následně je zapotřebí redukovat nejvíce pozitivní vlivy působící na
sledovaný prvek
Reálně řešené úlohy v praxi mohou klást na vývoj
prvků Xi ještě další podmínky. Jejich splnění a testování
vede ke kombinaci dosud popsaných analýz. Kromě požadavku na udržení
minimální hranice MIN může být ještě zároveň požadováno nepřekročení
zvolené maximální hladiny MAX. Nutné informace pro analýzu feasibilního
prostoru jsou následující:
-
vybraný prvek
-
hladina vymezující minimální hranici feasibilního
prostoru MIN
-
hladina vymezující maximální hranici feasibilního
prostoru MAX

Obr.
3 Průběh vývoje uvnitř feasibilní plochy vymezené minimální a maximální
hladinou. V intervalu vybočení mimo definovanou oblast analýza rozhoduje o
tendencích dalších opatření. V případě překročení maximální
hladiny se bude jednat o redukční zásahy, v opačné situaci o pozitivní
vlivy
V tomto druhu analýzy opět funguje princip superpozice
analýz prvků skládající dohromady celkovou analýzu modelu . Princip analýzy
spočívá v odpovědi na otázku, zda vypočtený vývoj prvku Xi nevybočuje
v celém sledovaném období za zadaného prostoru. Tato oblast může být
vymezena dvěma základními hladinami MIN a MAX. Systém však navíc umožňuje
zadat hranice ve tvaru lomených křivek, sledující požadovaný vývojový
trend prvku Xi. Rozbor tak může testovat, zda vývoj prvku Xi
leží například v negativně se vyvíjecím prostředí nebo naopak, zda se
pohybuje v pozitivní feasibilní ploše . Závěry analýzy musí zpracovat a
reagovat na ně řízení modelu.
Vývoj prvků při základním propočtu bez jakýchkoliv
interních a externích zásahů probíhá naprosto neřízeně (spontánně).
Hodnotu standardu tak není možné dopředu prognózovat. Stejně tak koncová
hodnota vývoje Xi(t=n) je k dispozici až po ukončení výpočtu.
Požadavek dosažení zadané koncové hodnoty VALUE je pak v praxi velmi častým
problémem. Jeho řešení odhaluje potřebu kapacity nutnou k dosažení cílové
hodnoty.
Řešení problému se nabízí v manuálním postupu. Po
ukončení každého výpočtu by řešitel provedl analýzu koncové hodnoty
Xi(t=n) a na jejím základě rozhodl o dalším postupu. Pokud by
nedosahovala požadované limity MIN, MAX, musel by reagovat na závěry
rozboru a celý výpočet opakovat, až by analýza nepodávala návrhy k dalším
opatřením. Kolikrát by bylo nutné cyklus opakovat není možné na začátku
odhadnout. Je tak vidět, že manuální postup je značně neefektivní a čas
zpracování se značně prodlužuje.
Jiný postup řešení prostřednictvím metod typu Goal-Seek
nelze také prozatím uplatnit, neboť není k dispozici analytické vyjádření
matematické závislosti mezi počáteční Xi(t=0) a koncovou
hodnotou Xi(t=n). Situaci zde mohou ještě více komplikovat
externí nebo interní opatření popřípadě rizikové vlivy. Navržené řešení
využívá analýzu koncové hodnoty Xi(t=n), která pro svoji činnost
potřebuje následující informace:
-
vybraný prvek Xi
-
požadovaná koncová hodnota Xi(t=n)
-
přesnost s jakou má být cílová hodnota dosažena d.
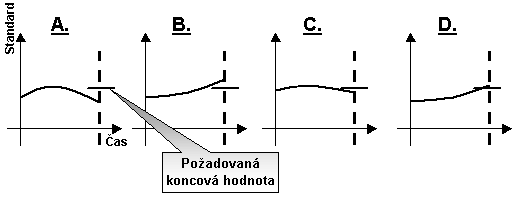
Obr. 4 Dopočet koncové požadované hodnoty Xi(t=n).
V krocích A. a B. analýza vyhodnotí situaci a doporučí pozitivní zásahy.
V kroku B. byla koncová hodnota Xi(t=n) překročena a je tedy
nutné vývoj redukovat. V posledním stadiu výpočtu je již dosaženo
koncové hodnoty přesně nebo s požadovanou přesností d a výpočet končí
Analýza koncové hodnoty standardu Xi(t=n) je
značně ovlivněna přesností výpočtu d. Vzhledem k numerické nepřesnosti
plovoucí desetinné čárky je obtížné skutečně dosáhnout zadané
hodnoty s nulovou odchylkou. Pokud by byl takový požadavek na nulovou
toleranci d
=0, znamenalo by tak citlivé reakce na výsledky analýzy, že by
již opatření z nich vycházející nebyla v praxi realizovatelná.
Simulovat alternativu absolutní přesnosti výpočet umožňuje zadáním
dostatečně nízké tolerance d
-> 0. Princip analýzy koncové hodnoty standardu pak spočívá
v testování absolutního rozdílu mezi vypočtenou hodnotu a zadanou
limitou. Pokud není diference v absolutní hodnotě menší než zadaná přesnost
výpočtu. podává o tom analýza informace, na které musí reagovat další
opatření. Výpočet se po zavedení nových vlivů opakuje a analýza
testuje nově vypočítané hodnoty Xi(t). Když je splněna podmínka
požadované přesnosti výpočtu, analýza již žádné příznaky pro úpravu
vnějších vlivů negeneruje a výpočet je ukončen.
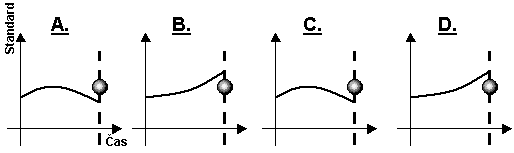
Obr.
5 Oscilace výpočtu okolo požadované koncové hodnoty VALUE. V krocích
A. a C. jsou na základě analýzy prováděny podpůrná opatření, v krocích
B. a D. dochází k redukci. Zásahy avšak nejsou natolik citlivé, aby byla
dosažena požadovaná přesnost d
a vypočtené hodnoty Xi(t) oscilují okolo požadované koncové
hodnoty VALUE
Analýza je schopna přesně určit zda již není příčina
k novým zásahům. Dále naznačí směr, kterým se mají intervence ubírat.
Jejich finální pozici a intenzitu však musí verifikovat řešitel úlohy.
Může se pak stát, že necitlivým zásahem nebude interval přesnosti d
dosažen a výpočet bude oscilovat okolo hodnoty blízké zadané přesnosti.
V takovém okamžiku je nutné zvolit citlivější formu zásahů nebo zvětšit
toleranci na přesnost výpočtu d.
Při opakovaném výpočtu by se již oscilace neměla opakovat a zadaná přesnost
by měla být dosažena. V opačném případě se úprava tolerance d
opakuje.
Závěry analýzy
Cílem správné analýzy výstupních dat by mělo být
nastínění směrů možných rezerv ve vývoji modelu, které by se měly
projevit ve snaze managementu o kvalitnější chování modelu. Pro řízení
všech procesů probíhajících v reálném čase jsou nutné informace o
jejich aktuálním vývoji. Na jejich základě mohou být následně
postavena manažerská opatření. Zdrojem těchto informací jsou právě
analýzy vývoje a skutečného stavu. Očekávaným výsledkem rozboru je správná
odpověď na analyzovanou otázku. V dosud popsaných postupech jsou zjišťovány
následující skutečnosti:
-
dochází k poklesu pod minimální hladinu MIN u
vybraného prvku Xi?
-
dochází k poklesu pod minimální hladinu MIN u všech
prvků Xi?
-
dochází k překročení maximální hladiny MAX u
vybraného prvku Xi?
-
dochází k překročení maximální hladiny MAX u všech
prvků Xi?
-
byla dosažena požadovaná hodnota VALUE?
-
nachází se vypočtená hodnota Xi(t) v
zadaném intervalu?
Odpovědi na tyto otázky jsou pro zavedení dalších
opatření nezbytně nutné a zpracované analýzy je dokáží uspokojivě
zodpovědět. Jistě je možné pokládat mnoho dalších otázek při řešení
různého druhu úloh. Systém je však navržen jako otevřený a případné
nové rozbory je možné do něho následně dopracovat. Závěry analýzy
zpracovává dále management a používá je již při vlastním řízení
modelu.





